This data set consists of 3D coordinates and knot types. These configurations lie within a cylinder with the vertices alternating between the two endcap disks. We analyzed configurations with even numbers of edges, from 6 through 30. There are 1,000,000 samples per number of edges. See the README.txt for more information. The image to the left has configurations with 6, 18, and 30 edges, respectively. The configurations form a +3.1, -10.124, and a knot type with crossing number 27. This data set is used in the following paper (which also appears in the previous two entries).

• Knotting spectrum of polygonal knots in extreme confinement
  Claus Ernst, Eric J. Rawdon, and Uta Ziegler
  To appear in J. Phys. A: Math. Theor.
  https://doi.org/10.1088/1751-8121/abf8e8
  
  

This data set consists of 3D coordinates and knot types. For each analyzed edge/radius pair, there are 100,000 configurations. See the README.txt for more information. The image to the left is a unit-length edge equilateral 30-gon rooted at the origin which is contained in a sphere of radius 2.0. It forms a negative trefoil. This data set is used in the following papers (all of which are listed in the previous entry as well).

• Relative frequencies of alternating and non-alternating prime knots and composite knots in random knot spaces
  Yuanan Diao, Claus Ernst, Eric J. Rawdon, and Uta Ziegler
  Experiment. Math., 27(4): 454-471, 2018.
  https://doi.org/10.1080/10586458.2017.1320239
  
  
• Total curvature and total torsion of knotted random polygons in confinement
  Yuanan Diao, Claus Ernst, Eric J. Rawdon, and Uta Ziegler
  J. Phys. A: Math. Theor., 51: 154002, 2018.
  https://doi.org/10.1088/1751-8121/aab1ed
  
  
• Average crossing number and writhe of knotted random polygons in confinement
  Yuanan Diao, Claus Ernst, Eric J. Rawdon, and Uta Ziegler
  React. Funct. Polym., 131: 430-444, 2018.
  https://doi.org/10.1016/j.reactfunctpolym.2018.07.028
  
  
• The knot spectrum of random knot spaces
  Yuanan Diao, Claus Ernst, Eric J. Rawdon, and Uta Ziegler
  In New Directions in Geometric and Applied Knot Theory, pages 205-237, Berlin, 2018. De Gruyter.
  https://doi.org/10.1515/9783110571493
  
  
• Knotting spectrum of polygonal knots in extreme confinement
  Claus Ernst, Eric J. Rawdon, and Uta Ziegler
  To appear in J. Phys. A: Math. Theor.
  https://doi.org/10.1088/1751-8121/abf8e8
  
  

This data set consists of 3D coordinates and knot types. For each analyzed edge/radius pair, there are 10,000 configurations. See the README.txt for more information. The image to the left is a unit-length edge equilateral 80-gon rooted at the origin which is contained in a sphere of radius 1.5. It appears to be a knot with crossing number 61. This data set is used in the following papers.

• The knot spectrum of confined random equilateral polygons
  Yuanan Diao, Claus Ernst, Anthony Montemayor, Eric J. Rawdon, and Uta Ziegler
  Mol. Based Math. Biol., 2: 19-33, 2014.
  https://doi.org/10.2478/mlbmb-2014-0002
  
  
• Relative frequencies of alternating and non-alternating prime knots and composite knots in random knot spaces
  Yuanan Diao, Claus Ernst, Eric J. Rawdon, and Uta Ziegler
  Experiment. Math., 27(4): 454-471, 2018.
  https://doi.org/10.1080/10586458.2017.1320239
  
  
• Total curvature and total torsion of knotted random polygons in confinement
  Yuanan Diao, Claus Ernst, Eric J. Rawdon, and Uta Ziegler
  J. Phys. A: Math. Theor., 51: 154002, 2018.
  https://doi.org/10.1088/1751-8121/aab1ed
  
  
• Average crossing number and writhe of knotted random polygons in confinement
  Yuanan Diao, Claus Ernst, Eric J. Rawdon, and Uta Ziegler
  React. Funct. Polym., 131: 430-444, 2018.
  https://doi.org/10.1016/j.reactfunctpolym.2018.07.028
  
  
• The knot spectrum of random knot spaces
  Yuanan Diao, Claus Ernst, Eric J. Rawdon, and Uta Ziegler
  In New Directions in Geometric and Applied Knot Theory, pages 205-237, Berlin, 2018. De Gruyter.
  https://doi.org/10.1515/9783110571493
  
  
• Knotting spectrum of polygonal knots in extreme confinement
  Claus Ernst, Eric J. Rawdon, and Uta Ziegler
  To appear in J. Phys. A: Math. Theor.
  https://doi.org/10.1088/1751-8121/abf8e8
  
  

This data set consists of the knot types of all Petaluma knots for 5, 7, 9, 11, and 13 petals. See the README.txt file in the zip file for information about how to decode what is there. The image shows the 7-petal +8.19 knot for the permutation (1,5,2,6,3,7,4). The top left is the polygonal petal knot configuration when viewed from above; the top right is the same configuration, but viewed from the side; the bottom left is a smoothed version on the same configuration; the bottom right is the +8.19 knot viewed as a torus (4,3) knot.

• A census of petal knots
  Addie McCurdy, Jason Parsley, Eric J. Rawdon, Brandon Tran, Elizabeth Whalen, and Grace Yao
  an arXiv link is forthcoming
  
  

This data set has the Alexander polynomial and determinants of all prime and composite knot types through crossing number 16. The documentation is in README.txt within the zip file. This data is not related to any particular publication. We just had it sitting around, so decided to post it.

Follow this link to see tight and knotplot knot configurations through 10 crossings aligned with respect to the principle axes of chirality as defined in the paper below. This site also includes some knots tightened with certain symmetries enforced and includes images, eigenvalues, and coordinates. This data is related to the following publication.

• Chirality of crooked curves
  Giovanni Dietler, Robert Kusner, Woden Kusner, Eric J. Rawdon, Piotr Szymczak
  arXiv of article
  
  

Follow this link to download the code to make pictures like the one on the left. The documentation for the program is there as well. This software is related to our work in the following publications.

• Knotting fingerprints resolve knot complexity and knotting pathways in ideal knots
  David A. B. Hyde, Joshua Henrich, Eric J. Rawdon, and Kenneth C. Millett
  J. Phys.: Condens. Matter, 27: 354112, 2015.
  doi:10.1088/0953-8984/27/35/354112
  
  
• Subknots in ideal knots, random knots, and knotted proteins
  Eric J. Rawdon, Kenneth C. Millett, and Andrzej Stasiak
  Sci. Rep., 5: 8928, 2015.
  doi:10.1038/srep08928
  
  

Follow this link to download the software to make pictures like the one on the left. The documentation for the program is there as well. This software is related to our work in the following publications.

• KnotProt: a database of proteins with knots and slipknots
  Michal Jamroz, Wanda Niemyska, Eric J. Rawdon, Andrzej Stasiak, Kenneth C. Millett, Piotr Sulkowski, and Joanna I. Sulkowska
  Nucleic Acids Res., 43(D1):D306-D314, 2015.
  doi:10.1093/nar/gku1059
  
  
• Knot localization in proteins
  Eric J. Rawdon, Kenneth C. Millett, Joanna I. Sulkowska, and Andrzej Stasiak
  Biochem. Soc. Trans., 41(2):538-541, 2013.
  doi:10.1042/BST20120329
  
  
• Identifying knots in proteins
  Kenneth C. Millett, Eric J. Rawdon, Andrzej Stasiak, and Joanna I. Sulkowska
  Biochem. Soc. Trans., 41(2):533-537, 2013.
  doi:10.1042/BST20120339
  
  
• Knotting pathways in proteins
  Joanna I. Sulkowska, Jeffrey K. Noel, Cesar A. Ramirez-Sarmiento, Eric J. Rawdon, Kenneth C. Millett, and Jose N. Onuchic
  Biochem. Soc. Trans., 41(2):523-527, 2013.
  doi:10.1042/BST20120342
  
  
• Conservation of complex knotting and slipknotting patterns in proteins
  Joanna I. Sulkowska, Eric J. Rawdon, Kenneth C. Millett, Jose N. Onuchic, and Andrzej Stasiak
  Proc. Natl. Acad. Sci. USA, 109(26):E1715-E1723, 2012.
  doi:10.1088/1751-8113/45/22/225202
  
  

Follow this link to see and download tight knots (i.e. minimized with respect to my definition of polygonal ropelength) at resolution one (i.e. the numbers of edges is about the same as their ropelengths). The polygons were ropelength-minimized using the freely available Ridgerunner package. This data is related to some ongoing projects, but is not a part of any published papers.

• Shapes of tight composite knots
  Jason Cantarella, Al LaPointe, and Eric J. Rawdon
  J. Phys. A, 45(22): 225202, 2012.
  doi:10.1088/1751-8113/45/22/225202
  
  
• Knot tightening by constrained gradient descent
  Ted Ashton, Jason Cantarella, Michael Piatek, and Eric J. Rawdon
  Experiment. Math., 20(1): 57-90, 2011.
  doi:10.1080/10586458.2011.544581
  
  

The database LinkProt catalogs all linking in the RCSB Protein Data Bank. The database updates weekly so that it includes to most recently deposited proteins. Users can upload their own protein chains for automated analysis. This work is in collaboration with a number of people. See this page for the current list of authors. The following article summarizes the capabilities of LinkProt.

• LinkProt: a database collecting information about biological links
  Pawel Dabrowski-Tumanski, Aleksandra Jarmolinska, Wanda Niemyska, Eric Rawdon, Kenneth Millett, and Joanna Sulkowska
  Nucleic Acids Res., 45(D1):D243-D249, 2016.
  doi:10.1093/nar/gkw976
  
  
  
  

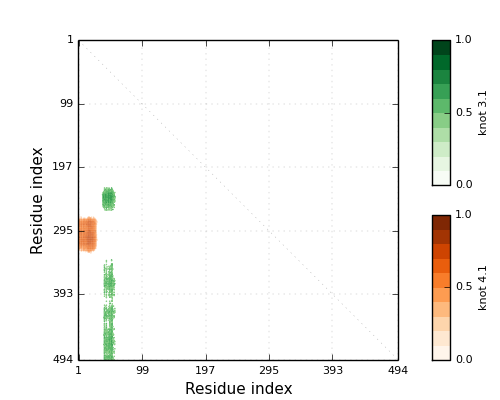
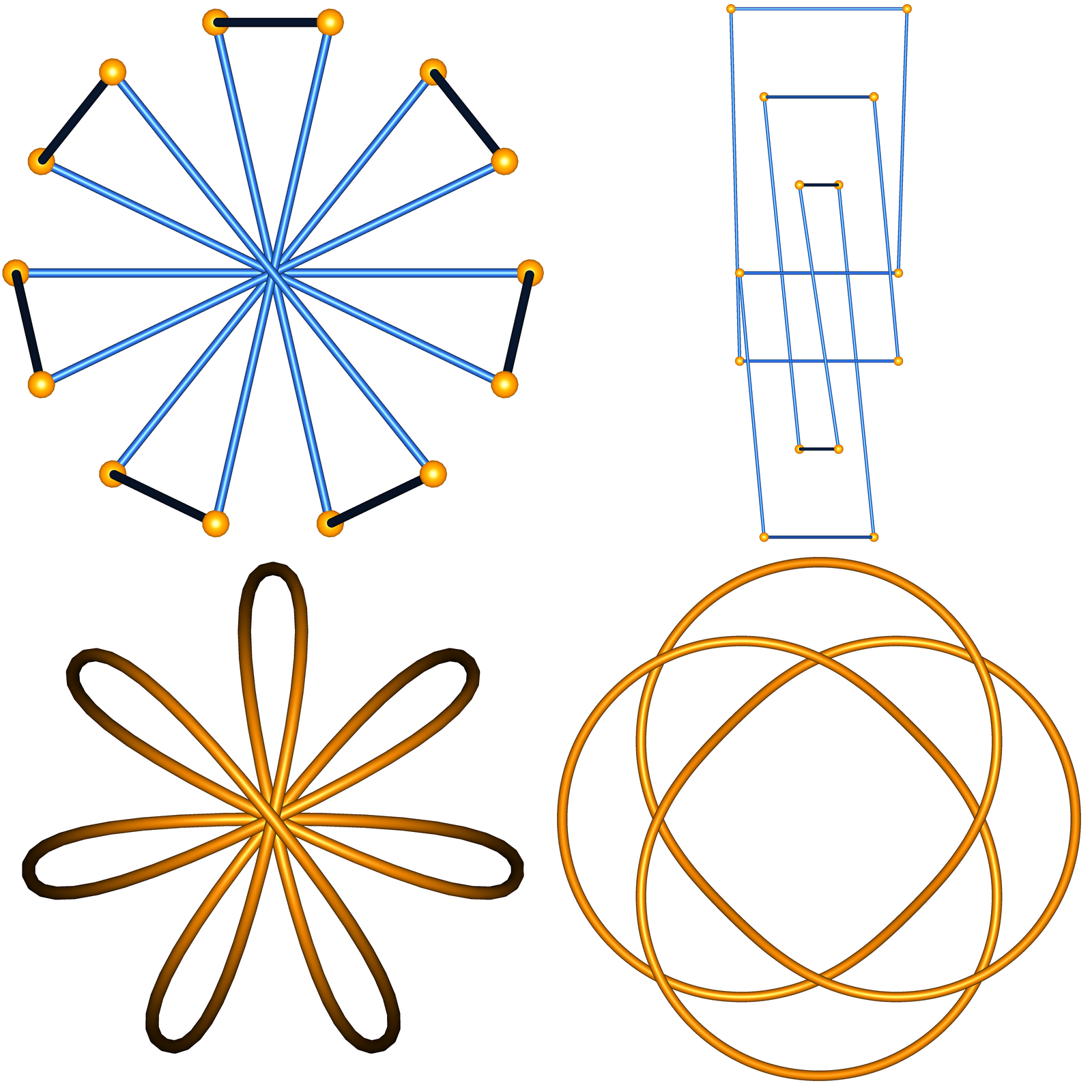
The database KnotProt catalogs all knotting in the RCSB Protein Data Bank. The database updates weekly so that it includes to most recently deposited proteins. Users can upload their own protein chains for automated analysis. This work is in collaboration with a number of people. See this page for the current list of authors. The following articles are related to our work with knotted proteins.

• KnotProt: a database of proteins with knots and slipknots
  Michal Jamroz, Wanda Niemyska, Eric J. Rawdon, Andrzej Stasiak, Kenneth C. Millett, Piotr Sulkowski, and Joanna I. Sulkowska
  Nucleic Acids Res., 43(D1):D306-D314, 2015.
  doi:10.1093/nar/gku1059
  
  
• Knot localization in proteins
  Eric J. Rawdon, Kenneth C. Millett, Joanna I. Sulkowska, and Andrzej Stasiak
  Biochem. Soc. Trans., 41(2):538-541, 2013.
  doi:10.1042/BST20120329
  
  
• Identifying knots in proteins
  Kenneth C. Millett, Eric J. Rawdon, Andrzej Stasiak, and Joanna I. Sulkowska
  Biochem. Soc. Trans., 41(2):533-537, 2013.
  doi:10.1042/BST20120339
  
  
• Knotting pathways in proteins
  Joanna I. Sulkowska, Jeffrey K. Noel, Cesar A. Ramirez-Sarmiento, Eric J. Rawdon, Kenneth C. Millett, and Jose N. Onuchic
  Biochem. Soc. Trans., 41(2):523-527, 2013.
  doi:10.1042/BST20120342
  
  
• Conservation of complex knotting and slipknotting patterns in proteins
  Joanna I. Sulkowska, Eric J. Rawdon, Kenneth C. Millett, Jose N. Onuchic, and Andrzej Stasiak
  Proc. Natl. Acad. Sci. USA, 109(26):E1715-E1723, 2012.
  doi:10.1088/1751-8113/45/22/225202
  
  

We tighten our knots using the freely available package Ridgerunner package. We have visualizations of the tightening process for knots and links The tight knot files can be found here in the VECT format. This arxiv article describes some of our results as well as how to interpret these images.

Some related articles include:

• The spectrum of tightly knotted flux tubes in QCD
  Roman V. Buniy, Jason Cantarella, Thomas W. Kephart, and Eric J. Rawdon
  Journal of Physics: Conference Series, 544(1): 012025, 2014.
  doi:10.1088/1742-6596/544/1/012025
  
  
• The tight knot spectrum in QCD
  Roman V. Buniy, Jason Cantarella, Thomas W. Kephart, and Eric J. Rawdon
  Phys. Rev. D, 89: 054513, 2014.
  doi:10.1103/PhysRevD.89.054513
  
  
• Shapes of tight composite knots
  Jason Cantarella, Al LaPointe, and Eric J. Rawdon
  J. Phys. A, 45(22): 225202, 2012.
  doi:10.1088/1751-8113/45/22/225202
  
  
• Knot tightening by constrained gradient descent
  Ted Ashton, Jason Cantarella, Michael Piatek, and Eric J. Rawdon
  Experiment. Math., 20(1): 57-90, 2011.
  doi:10.1080/10586458.2011.544581
  
  
  
  

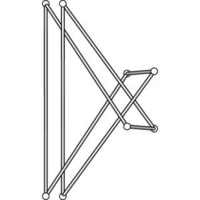
We have produced candidates for the minimum equilateral stick number using KnotPlot. This work is in collaboration with Rob Scharein and appears in the paper:

• Upper bounds for equilateral stick numbers
  Eric J. Rawdon and Robert G. Scharein
  In Physical knots: knotting, linking, and folding geometric
  volume 304 of Contemp. Math., pages 55-75, Providence, RI, 2002. Amer. Math. Soc..
  doi:10.1090/conm/304
  
  
  
  

Our original ropelength data used simulated annealing for ropelength minimization. The configurations, as well as a variety of spatial and topological measurements are available here. My former undergraduate researcher Michael Piatek did much of the work on the computations. The theoretical paper related to this work is:

• Can computers discover ideal knots?
  Eric J. Rawdon
  Experiment. Math., 12(3): 287-302, 2003.
  doi:10.1080/10586458.2003.10504499
  
  
  
  

This work explores ropelength optimization with a hard bound on curvature. Our hope is to capture the shape of ropelength minimizers in physical materials with curvature constraints. Visualizations with associated spatial characters are available as is the paper published in Physical Review E, 70:011803, 2004. This work was in collaboration with Greg Buck and Michael Piatek did much of the work on the computations.